衡水金卷先享题 2023届调研卷 生物(湖南专版)(三)3答案

衡水金卷先享题 2023届调研卷 生物(湖南专版)(三)3答案，九师联盟答案网已经编辑汇总了衡水金卷先享题 2023届调研卷 生物(湖南专版)(三)3答案的各科答案和试卷，更多九师联盟答案请关注九师联盟答案网。

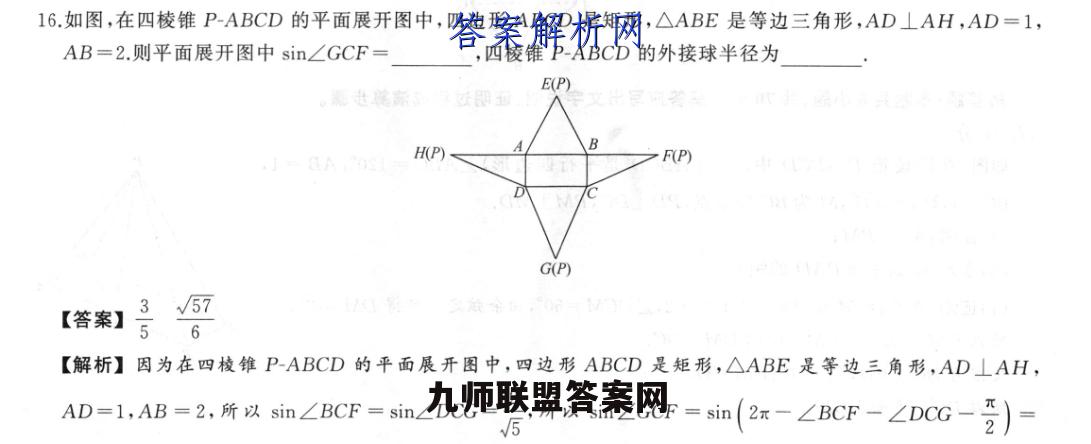
16.如图，在四棱锥P-ABCD的平面展开图中，四边形ABCD是矩形，△ABE是等边三角形，AD⊥AH,AD=1,AB=2.则平面展开图中sin∠GCF=,四棱锥P-ABCD的外接球半径为E(P)。彩世笔嘉近思国H(P)F(P)G(P)【答案】3-5√576【解析】因为在四棱锥P-ABCD的平面展开图中，四边形ABCD是矩形，△ABE是等边三角形，AD⊥AH,AD=1,AB=2,所以sin∠BCF=sin∠DCG=后，所以in∠GCF=sin(2x-∠BCF-∠D0G-）Sn2x-2∠DCG-受)=-as2∠D0G=2sin∠D0G-1=2X号-1=号如图，连接AC,BD交于点M,四棱锥P-ABCD的外接球球心为O,在四棱锥P-ABCD中，AD⊥AP,AD⊥AB,AP∩AB=A,所以AD⊥平面ABP,因为ADC平面ABCD,所以平面ABCD⊥平面ABP,取AB的中点H,连接PH,因为△PAB为等边三角形，所以PH⊥AB,因为平面ABCD∩平面ABP=AB,PHC平面ABP,所以PH⊥平面ABCD,设△ABP的外接圆圆心为N,连接OM,ON,则OM⊥平面ABCD,ON⊥平面ABP,则OM∥PH,可证得1w5ON∥MH,所以四边形OMHN是矩形，连接OD,因为△PAB为等边三角形，所以NH=3PH=了X3223,所以OM=3=S,设四棱锥P-ABCD的外接球半径为R,则R2=OM2+DM2=3十4=12，解得R76DBD￥在三棱锥P-ABC中，PA⊥平面ABC,AC⊥CB,PA=AC=BC=4.以A为球心，表面积为36π的球面与侧面PBC的交线长为【答案】π【解析】设以A为球心的球的半径为R,则4πR2=36π，解得R=3,如图，取PC中点H,因为PA=AC,所以AH⊥PC.又PA⊥平面ABC,BCC平面ABC,所以PA⊥BC.又AC⊥CB,AC∩PA=A,所以BC⊥平面PAC,又AHC平面PAC,所以BC⊥AH.又BC∩PC=C,所以AH⊥平面PBC,又PA=AC=BC=4,所以AH=2√2，PB=4√5.又交线上的点到H的距离为r=√32一(2√2)=1，作HE⊥PB,则△PEH△PCB,所EH PHCB=PB,所以EH=PH·CB2W2X4_2W6以PB43>1,所以球面与侧面PBC的交线为以H为圆心，半径为1的半圆孤，故所求长度为πX1=π.

15.在正四棱柱ABCD-A,B,C1D1中，AB=2,AA1=4,点O为底面四边形ABCD的中心，点P在侧面四边形BB,C1C的边界及其内部运动，若D,O⊥OP,则线段C1P长度的最大值为【答案】√652【解析】如图，当P位于点C时，因为四边形ABCD是正方形，所以AC⊥BD,由正四棱柱的性质可知，DD1」平面ABCD,因为ACC平面ABCD,所以DD1⊥AC,因为DD1∩BD=D,DD1,BD平面D:DBB1,所以OC⊥平面D1DBB1,D1OC平面D,DBB1,所以D1O⊥OC,因此当P位于点C时，满足题意；当点P位于棱BB1上的点P1时，若D1O⊥OP1,在矩形D1DBB1中，DD1=4,DO=BO=√2，因为∠P,OB十∠D1OD=∠D,OD+∠DD,0=90,所以∠P,OB=∠DD,O,图此Rt△P,OBRt△OD,D,所以有D0PBOB,即DDPB2√②￥BB=2,此时P,B=4-7=2又0P,∩0C=0,0P1,0CC平面0P,C,所以D,0LOP,C,故，点P在P,C上，线段C,P的最大值在C,P,或CC中取得，P,C,=√BC+BP=√4+49√6⑤>4，所以线段CP长度的最大值为6522DBPDB